Квантовый мир

13. Квантовая механика

Тепловое излучение

Из человеческой практики известно, что нагретые тела до определенной температуры приобретают свойства светиться. При охлаждении излучение прекращается видимой части спектра, т.е. за исключением инфракрасных лучей.

Для изучения теплового излучения было введено понятие лучеиспускательная способность тела, численно равная мощности излучения с единицы площади поверхности в интервале частот.

Так же была введена поглощательная способность, показывающая, какая доля энергии поглощается за единицу времени на единицу площади электромагнитными волнами в интервале частот.

В основном лучеиспускательная способность и поглощательная способность зависят от частот излучательных и поглощательных волн, температуры и химического элемента.

Наивысшей поглощательной способностью обладает абсолютно черное тело. У черного тела разница между испускательной и поглощательной способностями минимальна.

Полная лучеиспускательная способность абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры. При увеличении температуры вдвое, энергия, испускаемая телом, увеличивается в 16 раз.

С увеличение температуры основная часть энергии приходится на более короткие волны по сравнению с максимальной длиной волны, и она становится все более короткой.

Максимальная длина волны абсолютно черного тела обратно пропорциональна абсолютной температуре.

Типичным примером спектрального состава абсолютно черного тела является излучение нашего Солнца.

С точки зрения данной теории Солнце рассматривать как черное тело неправомерно. На Солнце происходят термоядерные реакции, т.е. происходит укрупнение химических элементов. Поэтому возникает дефект масс, т.е. часть массы вещества превращается в лучистую энергию. Температура поверхности Солнца обеспечивается за счет внутренней энергии его массы. В теории пеплового излучения принято, что абсолютно черное тело поглощает энергию извне, снаружи Солнца же практически получает ничтожную часть лучистой энергии.

Вся масса Солнца, ее агрегатное состояние представляет собой из себя плазму. Частицы этой плазмы, электроны и протоны перемещаются хаотически. На это хаотическое перемещение затрачивается колоссальное количество энергии. Вследствие этого энергия на лучеиспускание уменьшается.

Частично уже указывалось некоторые положения об излучении света с позиции теории «Квантовый мир».

Процесс поглощения и испускания веществом света это есть процесс контакта фотона той или иной длины волны с поверхности электрона, который находится на внешней оболочке атома. Этот контакт может происходить по двум сценариям. Если движение электрона совпадает с направлением движения фотона. В этом случае фотон контактирует с поверхностью электрона и передает свою кинетическую энергию, т.е. количество движения. Сам фотон перемещается с электроном с одинаковой скоростью. Электрон, получив лишнюю энергию, отходит от ядра атома на другую орбиту.

При этом отходе электрона от ядра производится работа в среде матричного вакуума, т.е. кинетическая энергия электрона переходит в потенциальную энергию среды вакуума. Затем возникает ответная реакция среды вакуума, и электрон прижимается на первоначальную орбиту. Фотон восстанавливали свою энергию. Но фотон одной длины волны, находясь на близком расстоянии с фотоном другой длины волны, среда вакуума прижимает их друг другу. И образуется фотон с другой длиной волны. При несовпадении движении движения фотона с движением электрона, этот фотон отскакивает от электрона. При этом длина волны не изменяется.

Поглощательная способность зависит от химического строения тела. Чем больше электронов на всех оболочках атома, тем больше увеличивается масса атома и тем больше поглощательная способность.

Так же поглощательную и лучеиспускательную способности определяет плотность вещества. Чем выше плотность материала, тем выше способность.

Поглощательная и лучеиспускательная способности зависят от строения структуры кристаллической решетки. Контакт фотонов с наружными электронами у атомов легких элементов протекает медленнее по причине больших расстояний между атомами.

Поглощательная способность тела может продолжаться вплоть до его разрушения и распада на излучения.

Лучеиспускательная способность ограничена. При понижении температуры до предела, который определяется средней плотностью лишних частиц среды в вакууме.

Закон Кирхгофа

Энергия, соответствующая лучеиспусканию вещества меньше энергии пошедшей на поглощение этим телом. Разница энергии пошла на колебательные движения атомов, т.е. на повышение температуры этого тела. В среде вакуума с большей величиной гравитации потребуется больше энергии на колебательные движения атомов и разница между лучеиспусканием и поглощением увеличится. Поэтому с увеличением гравитации отношение лучеиспускательной способности к поглощательной способности уменьшается.

Закон Стефана Больцмана

Это закон скорости перемещения энергии внутри материального тела, которая зависит от температуры, т.е. хаотического движения частиц атомов этого тела. Фотоны, перемещаясь в веществе, увеличивают объем атомов. Незначительное увеличение температуры ведет к резкому лучеиспусканию. Этот процесс возрастания лучистой энергии зависит от увеличения контактов фотонов той или иной длины волны с электронами, которые располагаются на наружных оболочках атомов.

С дальнейшим увеличением температуры наружные электроны атомов покидают свои орбиты, тем самым оголяются вторые орбиты атомов. Контакт фотонов резко возрастает с электронами, которых оболочек.

Закон Вина

Количество энергии, т.е. количество фотонов, контактирует с большим количеством электронов. И процесс возникновения фотонов на электроне с более большей длиной волны практически приостанавливается. То есть количество уже распределяется на большее число электронов. Следовательно, каждый электрон получает меньше энергии. Раннее в теории указывалось, что в среде вакуума существует определенная плотность фотонов различной длины волны. Это плотность практически не меняется и является причиной внутренней упругости среды вакуума. Поэтому с увеличением температуры все большее число электронов испускают фотоны с меньшей длиной волны.

Большой вклад в теорию теплового излучения внес Макс Планк. Он высказал идею поглощения и испускания света порциями- квантами. В своей теории он сохранил связь электромагнитной теории света с законами классической волновой оптики.

Показатель преломления света

Светом является электромагнитная волна. При переходе волны из вакуума или воздуха в диэлектрике свет отражается от поверхности этого материала. При этом происходит преломление этой волны. Отношение синуса угла падения к синусу угла преломления при этом переходе называется показателем преломления.

Посмотрим на это явление с позиций предлагаемой теории. Всякий диэлектрик, подвергшийся облучению фотонами той или иной длины волны, часть этих фотонов отражает, часть фотонов преломляется. Показатель преломления представляет удлинение пути фотона в среде вакуума. Среда матричного вакуума плотно заполняет объем в веществе, т.е. между частицами вещества. Фотон, двигаясь в этой среде, сталкивается или контактирует с атомами этого вещества (кристаллами, молекулами). Это самое удлинение и есть процесс преломления. А сам фотон перемещается в структуре вещества со скоростью света.

Часть фотонов проникает в вещество диэлектрика. Величина этого проникновения также связана с относительно большим расстоянием между частицами этого вещества. Чем плотнее вещество, тем больше коэффициент отражения.

Дисперсия

Далее рассмотрим явление дисперсии. Опыт показывает, показатель преломления света зависит от частоты колебаний световой волны.

Продолжим рассуждение с новых позиций. Узкий луч видимого света, т.е. белый, как известно из теории, представляет набор фотонов различной массы или длины волны. Фотоны, при прохождении кристаллической массы призмы, контактируют с электронами наружных оболочек атомов. Фотон, который произвёл контакт с электроном атома, утрачивает свое количество движения. Ответная реакция среды матричного вакуума восстанавливает количество движения. В момент восстановления количество движения фотона окружающая среда вакуума прижимает к этому фотону другой фотон, который находится в этот момент на поверхности этого электрона. В результате этого процесса возникает более тяжелый фотон. Этот утяжеленный фотон восстанавливает свою энергию, относительно легко проходит через внутреннюю грань призмы по тому же направлению, т.е. по инерции. При выходе из структуры призмы окружающее пространство фотон имеет наименьшее отклонение от своего прямолинейного пути в призме. Фотоны видимого света с наименьшей массой так же проходят внутреннюю грань призмы, но при выходе из нее откланяются от своего прямолинейного пути с наибольшим отклонением. Причина этому является масса фотона. При столкновениях более легких фотонов с электронами углы отклонения фотонов от своих траекторий оказываются большими по сравнению столкновениями более тяжелых фотонов. Это естественно, легкий фотон меньше отклоняет электрон от своей орбиты. А сам фотон, соответственно, больше отклоняется. А больший фотон больше отклоняет электрон от своей орбиты, а сам меньше отклоняется.

Столкновения фотонов с электронами происходят на всем пути в кристаллической массе призмы, от начала входа фотонов в призму и до самого момента их выхода.

То же самое происходит и с процессом утяжеления фотонов, т.е. утяжеление происходит с момента входа пучка видимого света и до самого их выхода из призмы. Если оранжевый фотон столкнулся с электроном и пошел не по направлению с оранжевым спектром, а его траектория оказалась с красным направлением. То среда матричного вакуума прижала красный и оранжевый фотоны друг другу и образовала инфракрасный спектр. И этот процесс продолжается вплоть до их выхода из кристалла

Движение свободной частицы

В квантовой механике рассматривается два случая движения частицы: когда на частицу не действуют никакие силы или частица находится под действием нескольких сил. У частицы, движущейся под действием нескольких сил, полная энергия оказывается величиной квантованной

В новой теории указывалось, что движение частицы представляет процесс раздвижения частиц среды матричного вакуума на объем равный объему движущейся частицы. Процесс раздвижения во времени зависит от скорости этой частицы.

Как охарактеризовать частицу? Она может быть различна по массе, химическому составу. Как правило, форма у них – шарообразная. По массе частицы могут очень сильно отличаться. От космических объектов до частиц нейтрино. Нужно отметить, что нейтрино волны де Бройля не имеет. Вещество с химическими свойствами помимо объема имеет волну де Бройля, равную половине массы этого объема. Этот объем волны де Бройля перемещается вместе с объемом свободной частицы. Фотоны той или иной длины волны имеют волны де Бройля, но частицы этой волны не передвигаются вместе с фотоном.

Отсюда можно сделать вывод, что свободной частицы в природе найти нельзя, Даже относительно неподвижные частицы матричного вакуума контактируют с окружающими ее частицами.

Частица в потенциальной яме и ее прохождение через потенциальный барьер

В физике рассматривается задача, в которой частица находится в потенциальной яме и ее движение ограничено потенциальным барьером. Энергия частицы в этой прямоугольной ловушке не может быть произвольной, а может быть только квантованной величиной.

Применительно к электрону эти энергии называются уровнями энергии. А числа, определяющие эти уровни, называются квантовыми числами. Электрон сколь угодно долго может находиться в стационарном квантовом состоянии в отсутствии внешних воздействий. Густо расположенные энергетические уровни образуют квазинепрерывные уровни.

Явление прохождения частицы сквозь потенциальный барьер называется туннельным эффектом. Для описания этого явления было введено понятие прозрачности потенциального барьера. Экспериментальное подтверждение этому служит явление холодной эмиссии электронов из металлов.

Ответим на вопрос, почему электрон находится на определенной орбите, т.е. находится в потенциальной ловушке?

Электрон, вращаясь на орбите вокруг ядра, имеет спин. Линейная скорость этого вращения равна половине скорости света. Помимо своей массы к электрону среда матричного вакуума прижила волну де Бройля, которая равна половине его массы. В свою очередь и ядро имеет спин и волну де Бройля. От двух потоков электрона и протона между ними возникает отталкивающий момент. Но электрон не покидает протон. Среда матричного вакуума прижимает электрон к ядру. Причина этому является напряженность, созданная тем, что электрон и протон занимают на 1/9 часть больше объема в среде вакуума. Получив квант энергии, т.е. кинетическую энергию фотона, электрон может занять другой уровень энергии. Чем дальше электрон находится от ядра, тем слабее среда вакуума прижимает электрон к ядру согласно закону квадрата расстояния. И для потенциального ящика макроскопических размеров эта напряженность ничтожна мала.

Движение электрона вокруг ядра определяется полностью средой матричного вакуума. Электрон постоянно совершает работу против частиц среды вакуума. При своем движении раздвигает ее, отдавая свою кинетическую энергию в потенциальную энергию окружающим частицам среды матричного вакуума. Совершив работу, частицы среды вакуума, восстанавливают его кинетическую энергию, и процесс продолжается относительно бесконечно.

В явлении холодной эмиссии электрон при очень малой напряженности электрического поля, т.е. при незначительном увеличении давления своеобразного электронного газа, получает от него порцию кинетической энергии. Который достаточно, чтобы электрон смог преодолеть силу давления на его среды матричного вакуума и покинуть свое ядро.

Водородоподобные системы по Бору. Атом Резерфорда

Резерфордом был поставлен опыт по прохождению альфа частиц через тонкие металлические пластинки из золота. Эти частицы были положительно заряженные с зарядом 2е. Масса этой частицы состояла из четырех масс атома водорода.

В результате опыта большинство альфа частиц сохраняли направление движения или на небольшой угол откланялись. Некоторые частицы откланялись на угол 150 градусов.

Объяснение было дано с точки зрения ядерной модели атома. Так же Резерфорду удалось установить зависимость альфа частиц, рассеянных на определенный угол и числом положительных зарядов в ядре. Было доказано, что число положительных зарядов в ядре равняется половине атомного веса. Таким образом, получала экспериментальное подтверждение идея Резерфорда.

В новой теории заряд рассматривается как отталкивающий момент между спинами ядра и электрона. В структуре я ядра входит половина нейтронов. Спины у нейтронов в отличии от протонов не имеются. Окружная скорость ядра составляет около световую величину.

Для дальнейшего рассуждения необходимо вернуться к началу развития Вселенной, в данном случае, к моменту взрыва квазара. На поверхности сферы квазара и в среде вакуума вокруг него действует очень большая сила гравитации. В момент приобретения крутящих моментов протонами, окружающая среда вакуума прижимает их нейтронам. При образовании ядер масса увеличивается вдвое, а крутящий момент остается неизменным. Масса увеличивается за счет нейтрона, а количество движения крутящего момента протона остается прежним. Таким образом, можно сказать, что отталкивающий момент ядра или согласно классической физике заряд ядра равен половине массы ядра.

Спектр водорода

Физиками 19 века были очень хорошо вычислены линейчатые спектры испускания атома водорода. Затем тщательные исследования показали дальнейшие серии спектральных линий от инфракрасных до ультрафиолетовых областей.

Для преодоления противоречий дискретно-линейчатого спектра атома водорода.

С классическим подходом модели атома Резерфорда была предложена неклассическая теория Бора.

Описание электрона строилось в основном на классических законах физики, но были дополнены ограничениями в виде постулатов.

Первый постулат Бора заключается в том, что существуют стационарные состояния атома, где он не излучает энергии. Несмотря на то, что электрон имеет ускорение, электромагнитного излучения нет.

Второй постулат, что в стационарном состоянии атома электрон должен иметь квантованные значения момента импульса.

Третий постулат Бора устанавливает, что при переходе атома из одного стационарного состояния в другое испускается или поглощается один квант энергии.

Движение электрона по Бору по орбите в атоме водорода происходит под действием кулоновской силы притяжения электрона к ядру атома. Радиус первой орбиты электрона называется Боровским.

Энергия атома в некотором стационарном состоянии обратно пропорциональна квадрату главного квантового числа.

Рис. 13.1. Опыт Франка и Герца: 1 – накаленный катод; 2 – сетчатый электрод; 3 – анод; 4 – гальванометр

Первый и третий постулаты Бора были подтверждены опытом Франка и Герца.

Идея эксперимента заключалась в пучке электронов, ускоряемых в электрическом поле и проходящих через газ. При этом электроны испытывали соударения с атомами газа. Газ представлял пары ртути подавлением 0,1 мм рт.ст.

С накаленного катода испускались электроны на анод. Между катодом и анодом находился сетчатый электрод. Между этим электродом и катодом создавалось ускоряющее электрическое поле, а между сеткой и анодом – слабое замедляющее поле. Электроны имели упругие столкновения, которые не препятствовали анодному току при возрастании ускоряющего электрического поля. Другие столкновения – не упругие, при этом энергия электронов передается атомам ртути.

Согласно постулатам Бора каждый атом не может воспринять энергию в любом количестве и перейти на одно из возбужденных энергетических состояний. Первое это состояние определялось 4,86 эВ. Приобретя большую энергию, электроны испытывали не упругие столкновения, и отдает свою энергию атомом ртути. При этом электроны не могли преодолеть задерживающего поля и не достигали анода.

Таким образом, при напряжении между катодом и сеткой 4,86 В происходит падение анодного тока. Аналогично должно происходить при разности потенциалов 2 x 4,86 эВ; 3 x 4,86 эВ; 4 x 4,86 эВ; n x 4,86 эВ. Тем самым это явление подтверждает первый постулат.

Так же подтверждается третий постулат Бора в опытах Франка и Герца. Возбужденные атомы ртути стали источником ультрафиолетового излучения. Это излучение происходит тогда, когда возбужденный атом ртути переходит в основное нормальное состояние.

Продолжим дальнейшее рассуждение о постулатах Бора. Находясь в одном из стационарных состояний, атом не излучает энергии. Однако оптический электрон движется с нормальным ускорением. Причина этому является воздействие среды вакуума на этот электрон.

На изначально возникшие частицы атома: электрон протон, нейтрон постоянно действует среда вакуума. Она стремится прижать их друг другу. В результате этого процесса возник атом, который приобрел нулевое стационарное положение. Это есть Боровский радиус атома, где n = 1. Помимо этого существует и другие стационарные состояния атома. Для перехода из одного стационарного положения в другое стационарное необходима энергия в форме фотона или пучка фотонов, а также воздействие на атом окружающей среды матричного вакуума в виде материального тела. Это взаимодействие осуществляется контактом с электроном наружной оболочки. В результате атом переходит в другое стационарное состояние. И находиться в этом состоянии он может сколь угодно долго. Надо отметить, что скорость вращения электрона вокруг ядра остается неизменной. Время нахождения атома в стационарном состоянии определяется плотностью хаотически перемещающихся фотонов различной длины волны в среде вакуума, т.е. напряженностью гравитационного поля. При возрастании силы гравитации атом излучает квант энергии, и электрон переходит в первоначальное состояние.

Рис. 13.2. Атом водорода: 1 – ядро атома; 2 – орбита электрона; 3 – диаметр электрона с волной де Бройля

Согласно новой теории электрон имеет волну де Бройля, которая входит в его массу. Вращается электрон вокруг ядра по принципу перемещения материального тела в среде матричного вакуума. Передвижение электрона с волной де Бройля происходит циклами. Каждый цикл сопровождается раздвижением среды вакуума на диаметр электрона с волной де Бройля. Затем среда вакуума вытесняет его из этого объема, и он обратно передвигается на расстояние своего диаметра (рис. 13.2). Половина или какая-то часть цикла не может быть. Поэтому количество диаметров электронов с волной де Бройля укладывается целое число на орбите.

Электроны, испускаемые катодом, разгоняются электрическим полем. Эти электроны контактируют с наружными электронами атома ртути. Если энергия электрона, излучаемая с катода, не превышает 4,86 эВ, то происходит столкновения этих электронов с электронами наружной оболочки атома ртути. Эти электроны воздействуют на ядро атома ртути, и он сам получает толчок, т.е. перемещается в пространстве. Если энергия превышает 4,86 эВ, то разгоняемый электрон входит в структуру атома ртути. А атом ртути, получив количество движения, переходит в возбужденное состояние. Этот процесс во времени занимает очень короткий период. После этого атом переходит в одно из стационарных состояний. Физический смысл этого процесса заключается в возрастании массы атома ртути и его объема. Существует и обратный процесс. Когда атом ртути переходит из высокого энергетического стационарного состояния в более низкое стационарное состояние. Этот процесс сопровождается возрастанием плотности среды вакуума окружающей этот атом ртути, т.е. возрастанием гравитации на атом ртути.

Водородоподобные системы

Движение электрона в кулоновском поле ядра с зарядом в водородоподобном атоме описывается волновой функцией, удовлетворяющей стационарному уравнению Шредингера. Решение этого уравнения в сферических координатах дает результаты момента импульса электрона в атоме. Значение этих результатов квантуется по определенной формуле. Последовательное решение уравнения Шредингера так же приводит к энергетическим уравнениям электрона в атоме типа Бальмера – Ридберга.

Состояния электрона в атоме обозначается s, p, d, f. В s-состоянии при n = 1 электрон находится в основном состоянии. При этом волновая функция электрона является функцией только радиуса – r. Электрон, находящийся в s-состоянии, т.е. при орбитальном квантовом числе равным нулю, имеет момент импульса: L₀ = 0.

Пространственное квантование и спин электрона

Орбитальный момент импульса электрона и пропорциональный ему магнитный момент ориентированы перпендикулярно к плоскости орбиты электрона и направлены в противоположные стороны. Ориентация векторов этих моментов выбирается направлением в пространстве и расположением вектора момента импульса электрона под углом к этому направлению. Направление определяется внешним магнитным полем или направлением внутреннего магнитного поля атома.

Зоммерфельдом было получено правило квантования боровских орбит, согласно которому проекция вектора орбитального момента импульса электрона на внешнее магнитное поле принимает целочисленные значения h.

Рис. 13.3. Опыт Штерна и Герлаха: 1 – фотопластинка; 2 – электромагнит; 3 – щелевые диафрагмы

Измерения магнитных моментов атомов были проведены О. Штерном и В. Герлахом. Для этого опыта были выбраны атомы химических элементов первой группы периодической системы Менделеева, у которых орбитальные элементы компенсируют друг друга кроме одного внешнего электрона (рис. 13.3).

Сила, действующая на атом в неоднородном магнитном поле, численно определяется индукцией этого магнитного поля. Схема опыта заключалась в узком пучке атомов, проходящего через сильное неоднородное магнитное поле, направленное перпендикулярно к пучку. Большой величиной неоднородного магнитного поля была достигнута большая отклоняющая сила, действующая на атом. Отклонения атома фиксировались на фотопленке. Опыт показал, что момент импульса и магнитный момент атома принимают фиксированные ориентации в магнитном поле. Все атомы принимают в магнитном поле два ориентира, соответствующим двум возможным положениям магнитного момента. У атомов первой группы их моменты импульса и магнитные моменты совпадают с моментами электрона.

Проекция магнитного момента электрона на направление внешнего поля численно равна магнетону Бора.

Из опыта Штерна и Герлаха следует пространственное квантование момента импульса в магнитном поле. И подтверждается, что магнитные моменты электронов численно равны количеству «элементарных моментов», т.е. это есть дискретная природа явления.

Из этого так же следует. Что валентный электрон в s-состоянии имеет орбитальное квантовое число равное нулю. Но в этом состоянии l = 0, т.е. нет момента импульса. Отсюда возникает вопрос пространственное квантование, какого момента импульса проявляется в опыте Штерна и Герлаха? Ответом на этот вопрос явился опыт Эйнштейна и де Газа, где было показано наличие у атомов магнитного момента, вызванного внутриатомным движением электронов.

В 1925 году С. Гоудсмитом и Г. Уленбеком была предложена идея, что, электрон имеет собственный механический момент импульса, т.е. спин электрона. Физическое понятие электрона, как вращающегося заряженного шарика вокруг своей оси, приводит к противоречию с теорией относительности.

Таким образом, собственному моменту импульса электрона соответствует собственный магнитный момент.

Пространственное квантование момента импульса атома в магнитном поле приводит к наличию двух ориентаций.

Проекция собственного магнитного момента электрона равна магнетону Бора.

Тонкая структура спектральных линий

При изучении спектральных линий водородоподобных систем, атомов щелочных элементов была определена тонкая структура спектральных линий, т.е. линии спектров этих атомов являются двойными. Для желтой линии натрия разделение ее составляет 6 А. Одна длина волны 5890 А, следующая за ней 5895,9 А.

Предполагается, что разделение энергетических уровней электрона приводит к данному явлению. На энергию электрона оказывает влияние его спин и зависимость массы от скорости. Эту зависимость на энергию электрона была использована Дираком в своей теории.

В атомной физике существует понятие спин – орбитальное взаимодействие электрона, т.е. взаимодействие магнитного спинового момента с орбитальным магнитным моментом. На основании этого была создана векторная модель атома, где результирующий вектор взаимодействия орбитального момента электрона складывается с его спином. И называется вектором полного момента импульса.

Таким образом, из выше приведенного следует, что с учетом спина электрона его орбитальному моменту соответствует два энергетических уровня – называемым дублетным уровнем.

До развития П. Дираком релятивистской волновой механики А. Зоммерфельдом было предложено влияние релятивистской зависимости массы скорости на энергетическое состояние электрона в атоме. Движение электрона с релятивистскими скоростями приводит к тому, что к движению его по эллипсу в его плоскости прибавляется движение прецессии, т.е. его траектория вокруг ядра относительно этой плоскости смещается. Этот процесс объясняется добавлением энергии электрону за счет учета влияния релятивистских скоростей.

Эффект Зеемана и Штарка

В источнике света, помещенного между полюсами электромагнита, спектральные линии расщепляются на компоненты.

В простейшем варианте расщепление состоит из трех поляризованных компонент. Средняя компонента направлена вдоль магнитного поля, две крайние поперек. Спектральная линия, распространяющаяся вдоль, исчезает, две крайние оказываются поляризованными по кругу. Этот тип расщепления называется нормальным. Тот эффект был объяснен Г. Лоренцем.

Эффект Зеемана основан на явлении расщепления энергетического уровня электрона. При этом электрон имеет только орбитальный магнитный момент.

Если магнитное поле слабое, наблюдается сложный эффект. При этом происходит расщепление спектральных линий на множество компонент. Причина этого эффекта является то, что при уменьшении магнитного поля взаимодействие между орбитальным и спиновым моментами становится существенным по сравнению с взаимодействием этих моментов в сильном магнитном роле.

Рентгеновские лучи

Рентгеновские лучи это электромагнитные волны с длиной волны от 0,01 A до 800 A. Возникновение этих лучей происходит при торможении веществом быстрых электронов. Рентгеновские лучи обладают высокой способностью фотохимического и ионизирующего действия. Эти лучи подразделяются на два типа. Первый тип это белое рентгеновское излучение, представляющее сплошной спектр, который ограничен со стороны малых длин волн величиной λ_min.

Второй тип рентгеновских лучей называют – характеристические лучи, представляющие линейчатый спектр. Особенностью этих лучей является неизменность линейчатого спектра независимо от того, в каких химических соединениях находится данный атом химического элемента.

Линейчатые рентгеновские лучи состоят из небольшого числа серий. Так же очень отличительно, что у разных химических элементов обнаруживаются однотипные серии линий, отличающиеся тем, что у более тяжелых элементов одинаковые серии линий смещаются в сторону коротких волн.

Принцип Паули

Этот принцип исключения заключается: в любом атоме не может быть двух элементов, находящихся в двух одинаковых стационарных состояниях, определяемых набором четырех квантовых чисел – главного – n, орбитального – l, магнитного – m, спинового – m.

В атоме, состояние электрона которого характеризуется четырьмя квантовыми числами, не может быть больше одного электрона.

В атом, состояние электрона которого характеризуется тремя квантовыми числами, не может быть больше двух электронов.

В атоме, состояние электрона которого характеризуется двумя квантовыми числами, количество электронов определяется выражением:

Z (n, l) = 2 (2l + 1)

В атоме, состояние электрона которого характеризуется одним квантовым числом, количество электронов определяется выражением:

Z (n) = 2n²

Главное квантовое число определяет слой или оболочку, в которую входит определенное число электронов.

Электронные слои имеют буквенные обозначения: K, L, M, N, O, P, Т, т.е. K – слой, который соответствует ближайшему расположению к ядру. В атоме слои строго не разделены в пространстве. В атоме имеются круговые и эллиптические орбиты. Электроны могут находиться в промежуточном слое.

Рассмотрев основные положения атома водородоподобных систем в квантовой механике, подойдем к описанию этого атома с учетом новой силы, т.е. с учетом среды вакуума.

Движение электрона вокруг ядра атома обусловлено принципом перемещения материального тела в среде вакуума.

Природой возникновения орбитального момента импульса электрона является свойство среды вакуума – её упругость. Среда вакуума прижимает электрон к протону. При передвижении электрона на расстояние равное его диаметру по орбите, он раздвигает частицы среды вакуума, которые окружают по его площади сферы. Таким образом, эти частицы среды вакуума приходят в движение. Следующее перемещение на диаметр электрона так же сопровождается движением частиц среды вакуума. Этот процесс происходит по всей длине орбиты электрона. Это движение частиц среды вакуума по орбите является орбитальным магнитным моментом.

Электрон кроме движения по орбите имеет вращательное движение. Электрон имеет прижатые частицы среды вакуума, которые представляют волну де Бройля. Эта волна выглядит как диск. Спин электрона имеет около световую скорость, и прижатые частицы среды вакуума были выброшены в экваториальную часть вращающейся сферы. Таким образом, геометрическая фигура волны де Бройля это вращающийся диск. Но так как, согласно данной теории, движущиеся частицы среды матричного вакуума представляют магнитные линии, т.е. магнитное поле электрона. Таким образом, волна де Бройля и является собственным магнитным моментом электрона.

Орбитальный момент импульса электрона удерживает его на орбите в атоме в результате постоянного давления среды вакуума. Вектор орбитального момента импульса ориентирован по радиусу атома. Если атом сложный, то для каждого электрона орбитальный момент импульса проходит по его радиусу, соединяющего протон с этим электроном. Для каждого атома вектор орбитального момента импульса лежит в плоскости его орбиты. В сложном атоме результирующий вектор направлен перпендикулярно новой плоскости сферы атома.

Магнитный момент электрона направлен перпендикулярно его плоскости. В сложном атоме для каждого электрона его магнитный момент действует перпендикулярно плоскости орбиты для этого электрона.

Суммирующий магнитный момент всех электронов атома представляет сумму этих магнитных моментов. Магнитные моменты электронов компенсируют друг друга. В результате векторная сумма этих магнитных моментов направлена перпендикулярно плоскости сферы атома.

При помещении атома во внешнее магнитное поле его спин будет ориентироваться параллельно этому магнитному полю. Смысл этого явления заключается в том, что движущиеся частицы среды матричного вакуума внешнего магнитного поля воздействуют и ориентируют частицы среды вакуума, движущиеся в плоскости орбиты электрона.

В сложном атоме внешнее магнитное поле воздействует на частицы среды вакуума. Представляющие магнитные моменты электронов внешнего слоя атома. И спин атома главным образом ориентируется параллельно этому внешнему магнитному моменту.

В предыдущих главах говорилось об общих понятиях заряда. Теперь решим эту задачу с количественной стороны.

Для решения этой задачи необходимо рассмотреть понятие момента импульса или момента количества движения вращающегося твердого тела. В природе господствует шарообразная форма тел. Это может быть вещество с химическими свойствами, нейтрино, а так же и ядерное вещество, т.е. протон и электрон.

Для вещества с химическими свойствами момент импульса определяется физической величиной, равной произведению момента инерции на угловую скорость.

Известно, что твердые тела в природе встречаются в виде кристаллов. Объем протонов, электронов составляет меньшую часть от объема, который образуется из межатомного пространства и пространства самого атома. По новой теории это пространство занято частицами среды матричного вакуума. При придании телу количества движения при поступательном движении или момента количества движения при вращательном движении затрачивается энергия на движение масс протонов этого тела и на движение частиц среды вакуума, входящих в объем этого тела. Поэтому для материальной точки, движущейся по окружности радиуса – r, момент импульса равен произведению импульса на этот радиус:

L = mvr

Величина радиуса включает весь объем рассматриваемого тела.

Момент количества движения сферического тела определяется уравнением:

L = 2/5 · mvr²

Величина 2/5 · vr² показывает, во сколько раз больше затрачивается энергии на движение частиц среды матричного вакуума, представляющих массу волны де Бройля данного вращающегося тела по сравнению с его весом. Структура ядерного вещества состоит так же из частиц среды вакуума. Но это количество обыкновенных частиц вакуума по сравнению с этим же частицами, которые входят в массу волны де Бройля какого-то определенного тела, гораздо меньше в ядерном веществе. То есть частицы среды матричного вакуума массы волны де Бройля не подвергаются силе гравитации. Но в силу прижатия этих частиц к массе тела средой вакуума, затрачивается энергия на придание им скорости.

На основании этого, математический подход вычисления момента количества движения сферического тела из вещества с химическими свойствами, не правомерен для сферического тела из ядерного вещества.

Для определения момента количества движения ядерного вещества, необходимо напомнить при каких обстоятельствах протон приобрел спин. Под все усиливающим возрастанием давления окружающей среды вакуума объем квазара уменьшается. На поверхности квазара господствует очень большая сила тяготения. Преодолеть эту силу не в состоянии даже фотон.

Затем квазар взрывается, т.е. вещество квазара проламывается через окружающую его среду вакуума. Из недр квазара выбрасываются струи нейтронного вещества. Во время этого выброса нейтрон получил вращательное движение вокруг своей оси, т.е. спин. Скорость вращения сравнима скорость света. Но часть своей массы нейтрон не удержал, и таким образом образовались электроны, спины которых так же сравнимы со скоростью света.

Рис. 13.4. Экваториальная область протона расположена по направлению оси X

На основании этого можно принять, что материальная точка ядерного вещества протона, которая находится в экваториальной области, должна иметь скорость света. То есть плотность количества движения в этой экваториальной области должна превышать плотность среды вакуума, окружающей квазар. Но не все точки вращающегося протона имеют скорость света. Скорость вращения шара по мере приближения к оси вращения снижается. Допустим, экваториальная область протона расположена по направлению оси X (рис. 13.4). Тогда элементарные частицы вещества среды вакуума, расположенные от центра шара от 0 до X будут иметь значения от нуля до скорости света. Средняя скорость элементарных частиц по оси X будет равна:

Vх = с / 2

Средняя скорость элементарных частиц вещества, расположенных по оси Y, от нуля до Y₁ равна:

Vу = c / 2

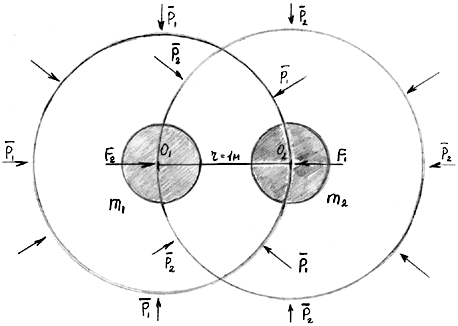
Рис. 13.5. Средняя скорость элементарных частиц среды вакуума по оси Z

Средняя скорость элементарных частиц среды вакуума по оси Z от Z₁ до 0 будет равна (рис. 13.5):

V_ср. = c / 2

Таким образом, средняя скорость всех элементарных частиц вещества шара будет по всем трем координатам равна половине скорости света

V = c / 2

Продолжим дальнейшее рассуждение о заряде. Момент количества движения протона это есть воздействие окружающей среды вакуума на этот протон. Это воздействие среды вакуума на движущейся протон заключается: в изменении направления движения протона.

Момент количества движения электрона это так же есть воздействие окружающей среды вакуума на движущейся электрон. Т.е. среда вакуума изменяет направление движения электрона. По этой причине электрон начинает движение вокруг протона на расстоянии от протона.

Вращающийся протон и вращающийся электрон порождают отталкивающие моменты между ними. Это расстояние между протоном и электроном и представляет собой физический смысл заряда протона и электрона. Величина этого расстояния уравновешивается окружающейся средой вакуума в порядке ответной реакции на возникающие моменты.

Классическим примером заряда является атом водорода. Этот атом в среде матричного вакуума представляет собой изотропное тело, т.е. на всю площадь его сферы действует упругость среды вакуума. Можно сказать, что действие среды вакуума представляет собой центростремительную силу, которая удерживает любой электрон на любой орбите любого атома. Орбитальное движение электрона описывает окружность некоторого радиуса, имея при этом определенную скорость.

Определим количества движения протона в атоме водорода:

L_пр. = М_пр. · V_пр. = М_пр. · V_ср. = 2,5·10^–19 кг·м/с,

где: М_пр. – масса протона; V_ср. – средняя скорость протона.

Количества движения электрона:

L_э = М_э · V_ср. = 2,7·10^–23 кг·м/с.

Следовательно, внутренняя упругость среды вакуума является причиной возникновения момента импульса электрона.

В данной теории указывалось, что вещество среды вакуума занимает на 1/9 часть объема больше, чем обыкновенные частицы среды вакуума. Это вещество составляет массу протона и электрона. Сумма их составляет атом, и этот увеличенный объем системы создает в среде вакуума напряженность, которая численно равна массе вещества. На создавшуюся напряженность следует ответная реакция среды вакуума. И по третьему закону И. Ньютона среда вакуума действует на этот напряженный объем. Величина этой реакции среды вакуума равна массе данного тела и вектор ее направлен противоположно вектору напряженности от вещества.

Наглядным примером реакции среды матричного вакуума можно рассматривать опыт Кавендиша. В этом опыте гравитационная постоянная определена экспериментальным путем. Рассчитаем величину гравитационной постоянной, используя основные положения предлагаемой теории.

Рис. 13.6. Опыт Кавендиша

Две частицы с массами М₁ = М₂ = 1 кг, каждая из которой создает в среде вакуума напряженность равную 1 кг (рис. 13.6). Напряженность в среде вакуума, образуемая этой массой, распространяется на площадь сферы радиусом R = 1 м. Вектор этой напряженности направлен по радиусу r от центра этого тела. Среда вакуума в свою очередь давит на эту площадь с абсолютно одинаковой силой, равной созданной напряженности. Эту напряженность можно рассчитать:

H₁ = М₁ / 4πR² = 7,96·10^–2 кг/м²

Таким образом, сила давления среды вакуума, т.е. реакция этой среды, на площадь сферы:

Р₁ = H₁

Аналогично напряженность, созданная в среде вакуума, от второго тела М₂ = 1 кг так же рассчитывается:

H₂ = М₂ / 4πR² = 7,96·10^–2 кг/м²

Рис. 13.7. Сила давления среды вакуума на площадь сферы от второго тела

Соответственно сила давления среды вакуума на площадь сферы от второго тела (рис. 13.7) равна:

P₂ = H₂

Частица М₂ лежит на поверхности сферы первой частицы (рис. 13.7). И она попадает под действие силы P₁. Масса М₂ прижимается средой вакуума к массе М₁.

Частица М₁ лежит на поверхности сферы второго частицы, и она попадает под действие силы P₂. И таким образом масса М₁ так же прижимается средой вакуума к массе М₂.

Сила среды вакуума, которая взаимодействует с массой частицы М₂, составляет n – часть от силы P₁. Эта n – часть силы давит на площадь сечения частицы М₂. Для этого необходимо найти эту площадь сечения частицы.

В рассматриваемой теории говорилось, что среда вакуума давит на лишние частицы среды вакуума. А ядерное вещество, т.е. электроны, протоны в основном состоят из лишних частиц среды вакуума. Сила гравитации действует не на всю площадь сечения атома, или какого – то материального тела, а в данном случае частицы, а только на ядро атомов. Поэтому нужно найти объем ядерного вещества частицы m₁ или m₂.

При расчете параметров Вселенной указывалось, какое количество лишних частиц среды вакуума входит в 1 кг массы, так же указывался объем этой частицы, отсюда определим:

V_{1 кг} = V_эф. · 1,5·10³³ = 1,08·10^–14 м³,

где V_{1 кг} – объем лишних частиц среды вакуума, входящих в один килограмм ядерного вещества.

Определяем радиус этого объема:

R_{1 кг} = R₁ = R₂ = 1,37·10^–5 м²,

где R₁ и R₂ – радиусы объемов ядерного вещества первой и второй частиц.

Находим площадь сечения объема ядерного вещества массой 1 кг.

S_{1 кг} = S₁ = S₂ = 5,89·10^–10 м²,

где S₁ и S₂ – площади сечений объемов ядерного вещества первой и второй частиц.

Сила давления P₁, которая взаимодействует с М₂ определяется как F₁:

F₁ = P₁ · S₂ = 4,69·10^–11 кг.

Сила давления P₂, которая взаимодействует с М₁ определяется как F₂:

F₂ = P₂ · S₁ = 4,69·10^–11 кг

Как видно из рис. 13.7 гравитационная постоянная складывается из силы давления P₁ и силы давления P₂, т.е. необходимо сложить F₁ и F₂:

Y_т = F₁ + F₂ = 9,38·10^–11 кг.

Обозначим Y_т – теоретическая гравитационная постоянная.

Расхождение Y_т с Y – экспериментальной можно объяснить влиянием окружающей массы на первую и вторую частицы.

Таким образом, можно сделать вывод, что гравитационная постоянная эта сила – реакция среды вакуума на вещество с химическими свойствами массой 1 килограмм.

Атом водорода

Аналогично опыту Кавендиша среда вакуума действует на все тела, как на Земле, так и во всей Вселенной.

Рассмотрим действие матричного вакуума в атоме водорода. Напряженность, созданная массой ядра водорода в среде вакуума, равна:

H_я = 1,6·10^–27 кг

На первой орбите в атоме напряженность определяется:

H_я = М_я / 4πR²_бор = 4,77·10^–8 кг/м²

Такая сила давления среды вакуума будет действовать на площадь сферы Боровского радиуса в атоме водорода, т.е.:

P_я = 4,77·10^–8 кг/м²

Электрон находится на площади этой сферы и прижимается силой P_я.

Объем ядерного вещества в электроне будет равен:

V_э = V_м.в. · 1370 = 1,02·10^–44 м³

Отсюда площадь сечения лишних частиц среды вакуума, входящих в этот объем, определяется как:

S_э 4πR_э² = 5,6·10^–30 м²

Сила давления среды вакуума, созданная массой электрона, будет гораздо меньше Р_я, поэтому силой Р_э можно пренебречь.

Определим силу среды вакуума, действующую на электрон:

F = P_я · S_э = 2,7·10^–37 кг

При вычислении гравитационной постоянной Y_т оказалось больше Y – экспериментальной:

р = Y_т / Y = 1,4

Провести эксперимент по измерению силы взаимодействия двух масс по 1 кг без влияния массы Земли практически невозможно. Поэтому целесообразно использовать коэффициент при расчетах, тогда сила, действующая на электрон в атоме водорода равна:

F_р = F / р = 2,7·10^–37 / 1,4 = 1,9·10^–37 кг

В опыте Кавендиша масса первой и второй частиц имеют нейтральные заряды, которые на расстоянии 1метра не влияют друг на друга.

В атоме же водорода заряд является основной характеристикой стабильности атома.

Выше было предложено, что зарядом является спин, т.е. его крутящий момент равный 2,5·10^–19 Дж/с и представляющий собой диск. Если бы вокруг атома была бы пустота, то атом бы распался на элементарные частицы среды вакуума. Но реакция среды вакуума адекватно действует своей массой, т.е. своей упругостью на этот крутящий момент и придает ему геометрическую форму диска. При вращении ядра, частицы его составляющие раздвигают частицы среды вакуума, т.е. совершают работу на расстоянии Боровского радиуса. Поэтому напряженность, создаваемая в среде вакуума ядром атома, равна по величине крутящему моменту протона. Сила гравитации ядра складывается главным образом из его спина и во вторую очередь из массы лишних частиц среды вакуума, входящих в протон.

Таким образом, напряженность, создана в атоме водорода его крутящим моментом, выражается как:

Н = 2,5·10^–19 кг

Напряженность, созданная в Н = 1,6·10^–27 кг массой ядра без учета спина. И как видно при сравнении Н_вод и Н_я их величины напряженностей сильно отличаются.

Определим силу давления среды вакуума Боровского радиуса в атоме водорода с учетом величины напряженности, созданной главным образом, крутящим моментом ядра:

Р_вод = Н_вод / 4πR²_бор = 7,1 кг/м²

Давление среды вакуума, созданное массой ядра, равно Р_я = 4,77·10^–8 кг/м², давление, созданное его крутящим моментом, равно Р_вод = 7,1 кг/м².

Из выше приведенного, можно сделать вывод, что величиной Р_я в практических расчетах можно пренебречь. Но не в теоретических расчётах, так как напряженность, создаваемая массой всей Вселенной, является движущей силой ее цикла развития.

Далее рассчитаем силу давления среды вакуума, девствующую на электрон на Боровском радиусе от ядра с учетом крутящего момента и с поправкой на поле тяготения Земли, т.е. коэффициента.

F_вод = P_вод · S_э · р^–1 = 2,8·10^–29 кг

Принцип ионизации электрона

Для того чтобы электрон произвел отрыв от ядра, ему нужно придать кинетическую энергию, которая смогла бы преодолеть силу давления упругости среды вакуума. Электрон при своем движении в атоме практически находится в каждой точке на площади сферы Боровского радиуса. И придать электрону энергию отрыва проблематично.

Если отрыв произойдет с n-орбиты электрона при:

W_n = L_l,

где:
W_n – энергия электрона на n-орбите;
L_l – момент импульса электрона

то будет наблюдаться явление туннельного эффекта. Чтобы электрон стабильно отрывался от атома, необходимо воздействие W энергии на каждую площадь сечения электрона, образуемая лишними частицами среды вакуума, входящих в его структуру.

Определим, сколько таких площадей сечения электрона укладывается на площади сферы для Боровского радиуса:

N = S_бор / S_э = 6, 25·10⁹,

где:
S_бор – площадь сферы Боровского радиуса;
S_э – площадь сечения электрона из лишних частиц.

Рассчитаем энергию ионизации W электрона:

W_ион = F_вод · N = 1,75·10^–19 кг,

где F_вод = L_l – это сила, действующая на электрон, равна моменту импульса электрона по теории Бора.

Опыт Штерна и Герлаха

Продолжим описание этого опыта и дадим объяснение действия силы на атомы в сильном магнитном поле. В процессе прижатия окружающей средой вакуума электрона к протону, их оси вращения ориентируются относительно друг друга параллельно. Направления движения спинов окружающая среда вакуума не изменяет.

В одном случае спины протона и электрона направлены по часовой стрелке. В другом случае при образовании атома спин протона может быть направлен по часовой стрелке, а спин электрона ориентирован против часовой стрелки.

В первом и во втором случаях отталкивающий момент между протоном и электроном не изменяется. В первом случае, когда их спины направлены по часовой стрелке, объем атома максимально увеличивается, т.е. расстояние между центрами электрона и протона будет самое большое во всех энергетических состояниях атома. При этом увеличении объема несколько снижаются спины электрона и протона. Во втором случае, когда спины направлены в противоположные стороны, объем атома несколько меньше. Спины электрона и протона не изменяются. Попадая в сильное неоднородное магнитное поле, разные объемы атомов будут испытывать разное воздействие этого магнитного поля. Следовательно, будет изменяться поступательная скорость атомов. Одни атомы будут иметь скорость 100 м/с т.е. без изменения, другие атомы снизят ее. Таким образом, происходит отклонение атомов на разное расстояние на фотопластинке.

Явление тонкого расщепления спектральных линий наблюдаются у химических элементов.

В процессе поглощения атомом натрия спектральной линии длиной волны 5890,0 А происходит ее расщепление на 6 А с длиной волны 5895,9 А. В среде вакуума во всем ее объеме существует определенная плотность фотонов различной длины волны. Величина этой плотности постоянная. Она является причиной возникновения гравитации.

Фотоны с длиной волны 5890,0 А попадая на электрон атома натрия, совершают работу в среде вакуума. Атом выходит из стационарного состояния, и электрон переходит на более высокий энергетический уровень. Но на поверхность электрона кроме фотона 5890,0 А попадают фотоны с длиной волны ультрафиолетового излучения. Среда вакуума, ввиду того, что фотон 5890,0 А, фотоны ультрафиолетового излучения и фотоны с меньшей длиной волны оказываются на близком расстоянии, прижимает их друг другу и образует фотон с длиной волны 5899,0 А.

Поэтому в спектральных приборах наблюдается фотоны с длиной волны 5895,9 А.

В атоме натрия происходит увеличение длины волны на 6 А. Причина этому, являются

химические элементы. Чем больше по времени атом находится в возбужденном состоянии, тем больше фотон 5890,5 А находится на поверхности электрона и тем больше

фотонов различной длины волны попадают на эту поверхность, и среда вакуума успевает больше прижать масс фотонов в больший фотон.

Вторым доводом влияния спина электрона на его энергетический уровень служит явление процессии. Атом, перемещаясь в пространстве, представляет движущуюся систему, состоящую без протона и электрона. В свою очередь электрон имеет вращательное движение вокруг протона. И при этом вращательном движении электрон не попадает на свою первоначальную орбиту, т.е. орбита смещается относительно первоначальной орбиты. Поэтому движение электрона по орбите это есть сложное вращательное движение, представляющее собой сумму движений поступательного движения атома его вращательного движения вокруг ядра. Это движение электрона является движением по спирали. Возникает это движение в атоме, когда он находится относительно в свободном состоянии. Такое состояние можно отнести к газовым средам, где плотность вещества небольшая.

Швейцарским физиком Паули в 1942 году в основном было сформулировано строение электронных оболочек. В атоме не могут находиться более одного электрона, находящегося в тождественном состоянии хотя бы с одним электроном.

На орбите атома водорода находится один электрон. В пространстве находится большое количество. Свободных электронов и среда матричного вакуума неизбежно прижмет один свободный электрон к атому водорода. Но этот электрон покинет атом водорода, он будет отброшен волной де Бройля вращающегося электрона вокруг ядра. На площади сферы Боровского радиуса, в основном в области экваториальной части этой сферы, два электрона обязательно сблизятся, и будут взаимодействовать своими спинами. И один из них покинет орбиту, т.е. отталкивающий момент между ними превысит момент импульса электрона.

Таким образом, среда матричного вакуума не в состоянии прижать электрон к ядру водорода.

Следующий по таблице Менделеева идет атом гелия. Масса его увеличивается, так же увеличивается площадь сферы слоя K. Электроны, находящиеся в этом слое, размещаются дальше друг от друга. Отталкивающий момент между ними уменьшается и среда вакуума, преодолевая взаимодействие этих электронов, прижимает их к ядру. При размещении третьего электрона в слое K атома гелия, отталкивающие моменты двух электронов выбрасывают его в пространство. А среда вакуума не в состоянии прижать его к ядру и электрон оказывается свободным. В противоположность этому состоянию является атом лития. В этом атоме аналогично двумя электронами слоя K выбрасывается третий электрон. Но он не покидает атом, образует третий слой L. Причина этому является увеличение массы протона ядра. Вследствие этого увеличивается напряженность в среде вакуума. Ответная реакция среды вакуума на эту напряженность возрастает, и электрон не покидает атом лития.

В атоме неона L – оболочка оказывается полностью застроенной, причем два электрона выбрасываются в подоболочку 2S шестью электронами, которая среда вакуума удерживает в этом слое.

Дальнейшее рассуждение приводят к выводу, что количество электронов, находящихся в оболочках K, L, М и т.д. определяется балансом равновесия между отталкивающими моментами электронов, находящихся в одной из оболочек и среда вакуума способна удержать эти электроны на соответствующих орбитах, т.е. в слоях.

Рис. 13.8. Ответная реакция среды вакуума, которая окружает молекулу воды, на внутреннее количество движения ядер водорода, кислорода и электронов:
1 – давление окружающей среды вакуума; 2 – ядро атома кислорода; 3 – ядро атома водорода

Рассмотрим распределение электронов по оболочкам в молекуле воды (рис. 13.8).

Ядро атома кислорода и ядра атомов водорода относительно друг друга неподвижны. Эти ядра представляют молекулу воды. Крутящие моменты ядра кислорода и ядер водорода создают в среде вакуума напряженность. На это следует ответная реакция среды вакуума и прижимает эти ядра друг другу. Крутящий момент ядра кислорода выбрасывает в свою экваториальную часть ядра водорода. Молекула воды имеет две электронные оболочки. На L – оболочке среда вакуума удерживает четыре электрона. Она прижимает два электрона к ядру атома кислорода и два электрона к ядрам атомов водорода. Остальные шесть электронов выбрасываются на вторую орбиту.

Рис. 13.9. Молекула воды окружена волной де Бройля: 1 – горизонтальное скольжение; 2 – волны де Бройля молекул

Эта молекула воды приобрела форму диска. Окружающая среда вакуума молекулы друг другу в местах с наименьшими отталкивающими моментами, т.е. в полюсах этих дисков. Поэтому молекула воды стремиться рассредоточиться по горизонтальной поверхности относительно друг друга. Так как молекула воды окружена волной де Бройля, т.е. сверхтекучей средой вакуума, т.е. они скользят относительно друг друга (рис. 13.9).

Молекулы воды в экваториальной части дисков взаимно отталкиваются, но в полюсах этих молекул наименьшие отталкивающие моменты. Горизонтальное давление – скольжение исчезает тогда, когда молекулы воды рассредоточиваются по горизонтальной поверхности в один слой, т.е. толщина слоя будет равна толщине одной молекулы. В этом случае отталкивающие моменты между молекулами волы достигают наивысшего предела. Согласно данной теории, у воды, которая располагается по горизонтальной поверхности, между молекулами большое расстояние, превышающее величину самой молекулы. То в этом случае вода приобретает фазу водяного газа.

Большой вклад в изучение электронных оболочек атома внес В. Рентген открытием своих лучей.

Природа возникновения рентгеновских лучей определяется торможением быстрых электронов веществом. Энергия, приданная электрону, находится в диапазоне 10⁴...10⁵ и выше.

Электроны, испускаемые катодом, находятся в свободном состоянии, в том понятии, что они не испытывают влияния спина ядра. То есть они находятся вне системы атома. В среде вакуума, в пространстве, где электрон набирает скорость, находятся фотоны различной длины волны.

Среда матричного вакуума аналогична как в системе атома, неизбежно прижимает фотоны различной длины волны к электронам. Но эти электроны не испытывают отталкивающего момента ядра атома. И фотоны, прижатые средой вакуума, остаются на поверхности электрона до их торможения веществом. При торможении этих электронов веществом, среда вакуума прижимает электроны с прижатыми к нему фотонами к атомам этого вещества. Оказавшись в системе атома, эти электроны стали ощущать воздействие отталкивающего момента ядра. И раньше прижатые фотоны покидают электрон. Это и есть пучки рентгеновских лучей.

Чтобы электрону разогнаться, т.е. получить кинетическую энергию, пройти путь от катода до анода требуется некоторое время. За этот промежуток времени среда вакуума успевает прижать определенное количество фотонов. Вот это количество фотонов и зависит от времени прохождения электронов до анода. Чем больше будет создано электрическое поле в вакуумной трубке, тем электрон быстрее пройдет расстояние от анода, тем меньше среда вакуума успеет к нему прижать количество фотонов, и вновь образовавшиеся фотоны на поверхности электрона будут меньше, т.е. длина волны рентгеновских лучей будет минимальной. Уменьшим электрическое поле, электрон больше будет находиться в вакуумной трубке, среда вакуума больше прижмет к нему фотонов и длина рентгеновских лучей будет больше. Это и есть понятие некоторой границы λ_min называемой границей сплошного спектра.

Рентгеновские лучи со сплошным спектром образуются от материала антикатода. На электроны химических элементов, имеющих на внешних электронных оболочках большое количество электронов, попадание постоянных лишних частиц среды вакуума меньше, чем на один валентный электрон. Поэтому укрупнения фотонов на внешних электронах тяжелых элементов уменьшается. Вследствие этого образуется рентгеновское излучение с различными короткими длинами волн. Этот диапазон различных волн представляет белое рентгеновское излучение.

В атомах, имеющих небольшое количество электронов, на внешних оболочках, укрупнение фотонов на электронах увеличивается. Но различие коротких волн уменьшается. И образуется диапазон жесткого излучения, называемым характеристическим, т.е. со своим определенным линейчатым спектром конкретного химического элемента.

Рентгеновские лучи имеют большую проникающую способность. Они входят во взаимодействие с электронами K, L, М и др. оболочек. Но электроны этих оболочек очень мало взаимодействуют с постоянными лишними частицами в среде вакуума. Поэтому процесс укрупнения фотонов на K, L, М и др. оболочек маловероятен и квант излучения постоянный, т.е. определенный длины волны. Этот процесс является основанием метода определения химического элемента рентгеновскими лучами.

• 14. Атомное ядро

• Оглавление

Дата публикации:

16 ноября 2011 года